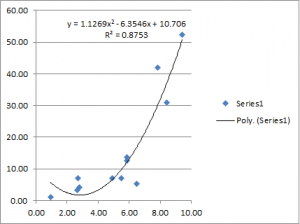
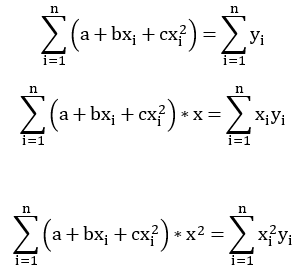The canonical way to tell whether an animal (or anything) is self-aware is the mirror-test. Put it in front of a mirror, if the animal recognize itself, then it’s self-aware; otherwise it’s not.
But then what exactly is self-awareness? What exactly does the mirror-test test? Can we make self-aware machines? I was pondering on this because I recently realized that vehicles (or in general any device) are considered dumb not only because they have no intelligence, but also because they are not self-aware.
Take a car for example, it’s considered dumb not only because it cannot make any intelligent decision on itself, but also because it will do things that are obviously against it’s own best interest as long as that’s the command from a human being. Would it be interesting if we can build a car that cares itself and avoids crashes and collisions out of its own interests?
Back to the mirror test. Essentially the test tests the ability of an animal to recognize oneself through visual signal of optical reflection. Let’s try to break it down by replacing non-essential part.
First of all, it seems that there’s no obvious reason we should limit ourselves to visual signal. It’s just one form of signal that a lot of animals can sense easily. A lot of other animals rely on other sensors. For example, bats are known to be able to tell its own ultra sound signal from others. If we’re not limited to visual reflection, then recognizing oneself through reflected/echoed signal is not that difficult. For example, if an device could simply broadcast its own identity through ultra sound like a bat.
We can build a device that broadcast its own identity through ultra-sound, let’s say the identity has a form of a GUID. Now, our device will be able to tell its own signal apart from other signals. Is that enough to be self-aware?
Most cars manufactured nowadays have more than one ultra sound radar built in. They beep when they sense the danger of crashing into something. It seems that it kind of self-aware, but not quite, right?
We have to take a closer look at the mirror test. When a self-aware animal first sees itself through a mirror, it has no prior knowledge about its own appearance in the mirror. Then how exactly does it come to the conclusion that the object inside the mirror is a visual representation of himself? The only possibility is, the animal actually learns that by experimenting.
Wikipedia actually has a full description of the mirror test being conducted the first time:
In 1970, Gordon Gallup, Jr., experimentally investigated the possibility of self
-recognition with two male and two female wild pre-adolescent chimpanzees (Pan
troglodytes), none of which had presumably seen a mirror previously. Each chimpanzee
was put into a room by itself for two days. Next, a full-length mirror was placed in
the room for a total of 80 hours at periodically decreasing distances. A multitude
of behaviors were recorded upon introducing the mirrors to the chimpanzees. Initially,
the chimpanzees made threatening gestures at their own images, ostensibly seeing their
own reflections as threatening. Eventually, the chimps used their own reflections for
self-directed responding behaviors, such as grooming parts of their body previously
not observed without a mirror, picking their noses, making faces, and blowing bubbles
at their own reflections.
From this description it’s obvious that the recognition is a learning process. This observation has several implications:
First of all, because it’s a learning process. It’s very flexible, very adaptive. The animal doesn’t have to stand still in front of a mirror to recognize itself. Even the physical appearance later changes dramatically, the animal will be able to recognize himself again very quickly.
In contract, if a device just broadcast our own identity, then in a noisy environment, then it may have difficulties. Or, if for some reason we have to change the identity, then we also have to change the verification logic.
Secondly, indeed we don’t have to limit ourselves to visual reflection. Voice will also do. Touching will also do. In fact, people that are born to be blind are able to recognize themselves by other senses. And we don’t think they are not self-ware.
Last, a very subtle prerequisite of such a learning process is, the animal has to know its own properties and boundary. Otherwise, the animal won’t be able to know a waving arm is its own or not (with or without a mirror). Every animal knows it’s own properties and boundary (This is my fur, this is my claw, etc), if we’re trying to design devices to be self-aware, we have to build this capability as well.
So by now I think we can define self-awareness as:
- Knows ones own properties and boundary;
- Able to learn ones own identity from experiments;