其实是泊松分布的经典应用:
已知某呼叫中心每小时会进ci个电话,每个电话平均时长为tp,则在任意给定时刻,并发电话的为x的概率服从泊松分布。此处假设不同的电话是完全独立事件。
并发电话为x的概率,等同于在tp时长内,进入x路电话的概率。在tp时长内,平均会进的电话数为tp*ci。因此,并发电话小于或等于x的概率为(excel公式):
POISSON(x,tp*ci,TRUE)
其中最后一个参数TRUE,表明这里计算的是并发电话小于或者等于x的概率;如果用FALSE,则只计算等于x的概率。
此公式可用于呼叫中心容量规划,比如:如果已知呼叫量和平均通话时长,则要确保容量在99%的情况下够用,则只需求x,使得POISSON(x,tp*ci,TRUE)>0.99。
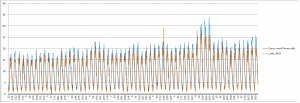
在某呼叫中心,把历史数据应用了一下,符合度很高:
其中横轴是时间,黄色为实际并发量,蓝色为按照0.999计算出的并发量上限。
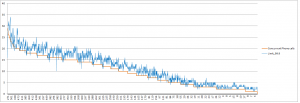
如果把横轴改成按照实际并发量排序,则得到:
可以看到实际并发量几乎总是在预计容量之下。几个实际并发量高于预计容量的情况,后来证实都是系统出了故障,导致客户竞相反复拨打,意味着不仅原来的参数不再适用,独立同分布的假设也不再适用。