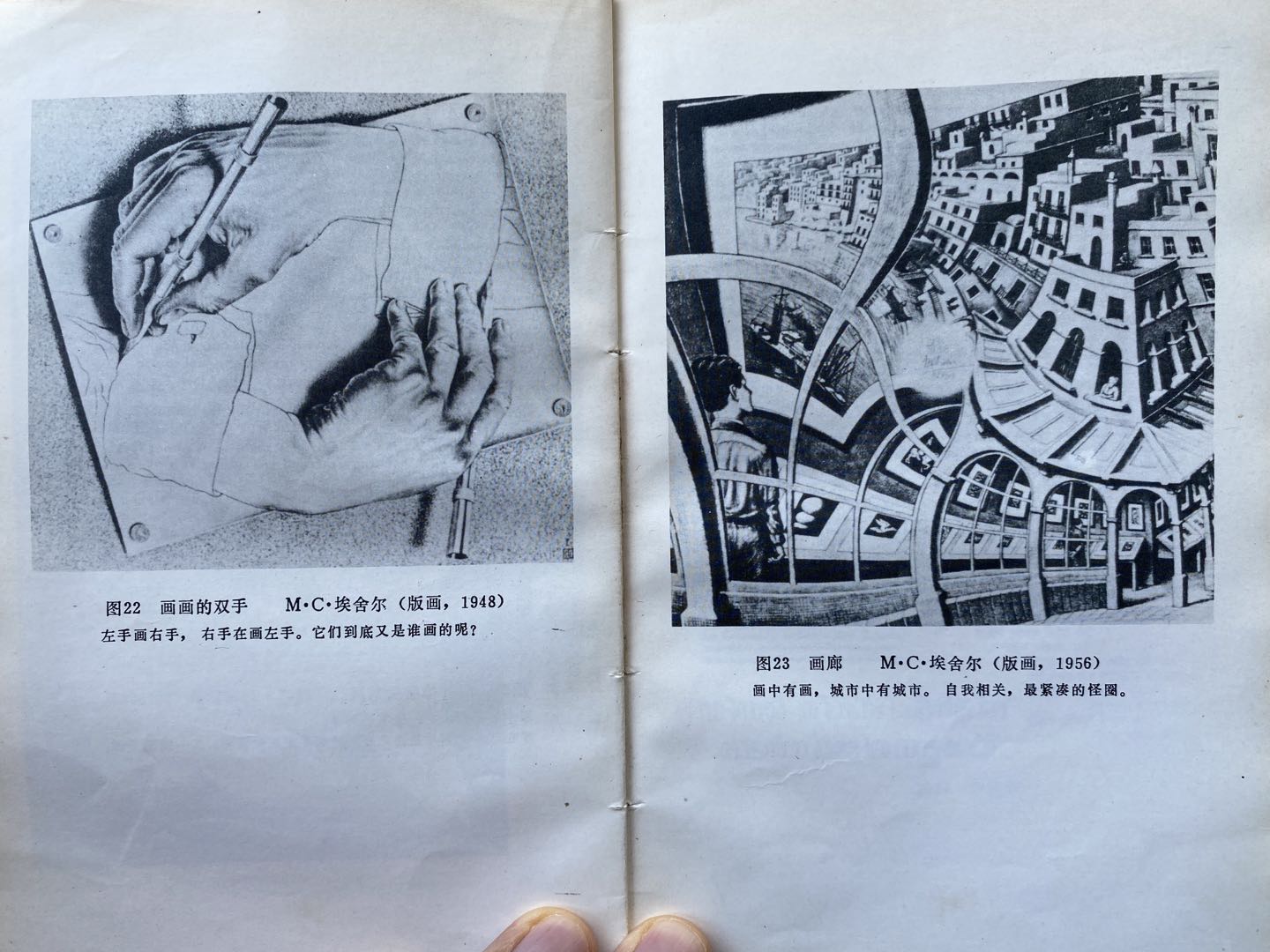
听说Escher,是在大学时候看到这本书:
这是Gödel, Escher, Bach: an Eternal Golden Braid一书的中文简译,本来就比较抽象艰深,再进行翻译和简化转述,文字看得半懂不懂,图片倒的确是看的津津有味。
右图就是我们要山寨的Print Gallery:
书虽然并未看懂,但我对哥德尔和埃舍尔一直感兴趣。北京有一个凤凰汇购物中心,内部有几个立面用了埃舍尔的画做装饰,初见时颇以为讶异,还跟好几个人介绍过。
 |
 |
但我对埃舍尔的作品的理解一直是,这些画作为数学家提供了一些灵感,从未想过这些画作本身可能蕴藏着真正的数学。直到2016年在podcast上看到一个Oxford的讲座:
https://podcasts.apple.com/us/podcast/the-secrets-of-mathematics/id852374699?i=1000420938867
Youtube链接在这里
简单地说,数学家通过仔细观察这副画作,发现埃舍尔通过一种数学变换(学电子信息的朋友可能很熟悉的保角变换),把一个缩放不变的图像(Droste Effect),变成了二维平面上的循环结构。
更详细的讲解见这里。
看完这个讲座,我就决定要自己做一个类似的作品来致敬埃舍尔,动起手来才发现非常不容易。
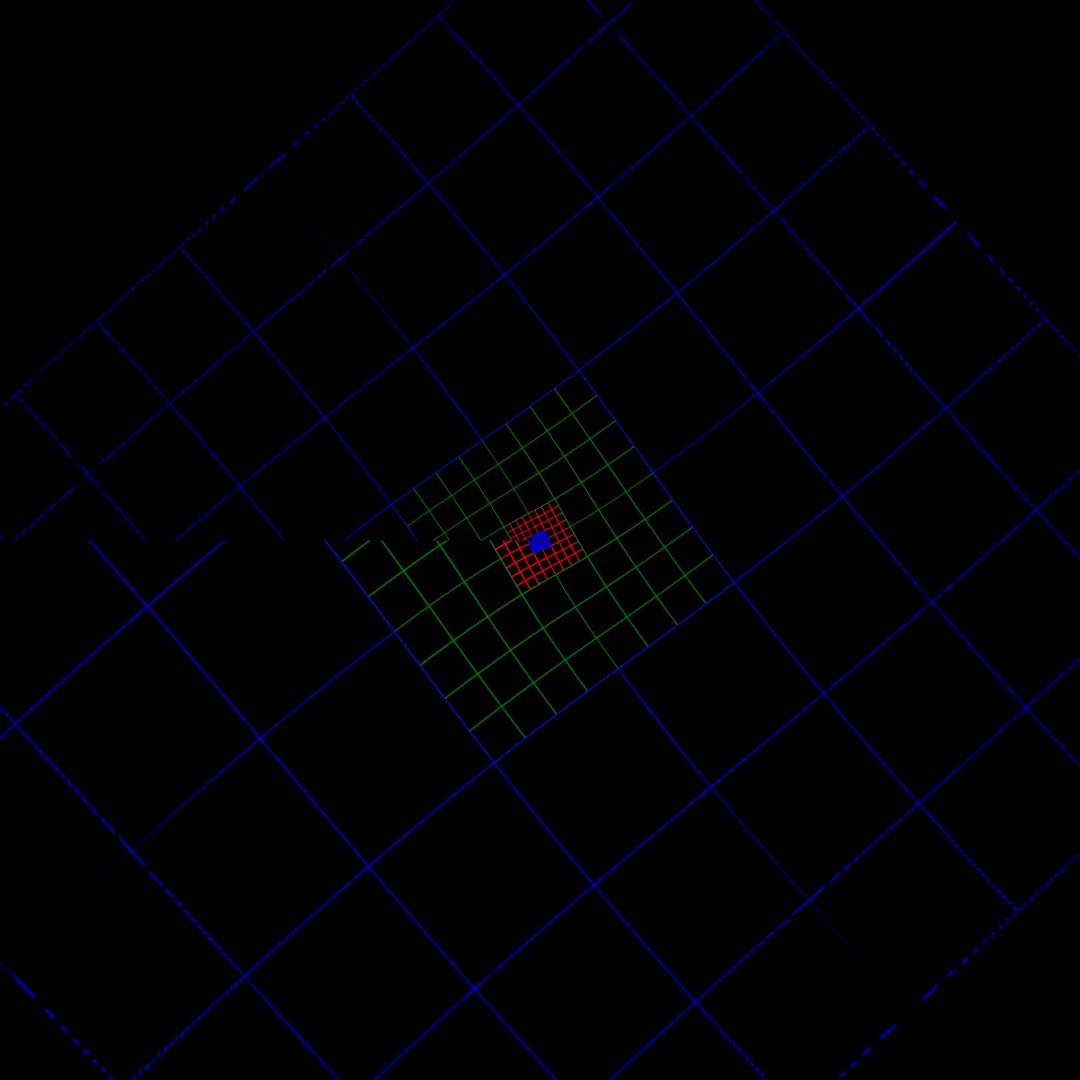
一开始我用的是OpenCV的remap函数。当时遇到的问题是,remap函数本来就不直观,加上变换矩阵确实复杂,而手头一时也没有合适的素材。所以一直停留在原理验证阶段。下图是2017年的成果。
可以看到实现了错位效果,但是没有实现内外层的对齐。后来发现是旋转角度取反正切的时候算成反余切了,所以一直对不上。最初的热情逐渐冷却,就放下来了。
到了2020年,彭罗斯获得了诺贝尔奖(物理学!),才又想起这个事情——彭罗斯及其父亲跟埃舍尔过从甚密,还在牛津给本科生开了一门课,就叫Eschermatics,埃舍尔数学。Chapman的讲座后面就是Penrose讲密铺和Escher的画。
这一次改用OpenCV的warpPolar函数,省得自己做变换矩阵了。但是带来的问题是,我们需要变换的图像在横轴和纵轴两个方向都是周期性的,而warpPolar函数在纵轴上只有0-2pi这一个周期,而在横轴上则没有周期,需要手动进行周期性延拓。
此外,由于数字图像天然是矩形的,对图像进行旋转之后,会在四个角形成黑块。这也需要进行处理。
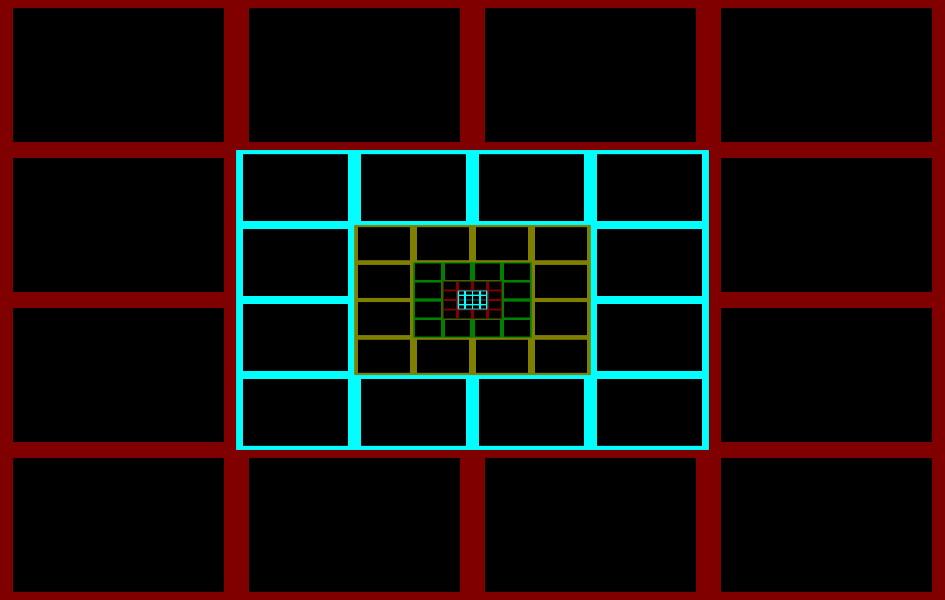
这些都处理完成之后,才得到这样的结果:
 |
 |
这一回,终于对齐了。代码完全跑通了。接下来是素材问题。
可以看到,经过变换之后的图像在边缘区域像素颗粒已经很明显。这还仅仅是16倍的Droste比例,要实现埃舍尔的256倍Droste比例,看来必须采用讲座中提到的分步法:拍4张照片,每一张比前一张放大4倍。变换之后分别对应一个区域,形状如右上图中的颜色分布。然后拼贴到一起。
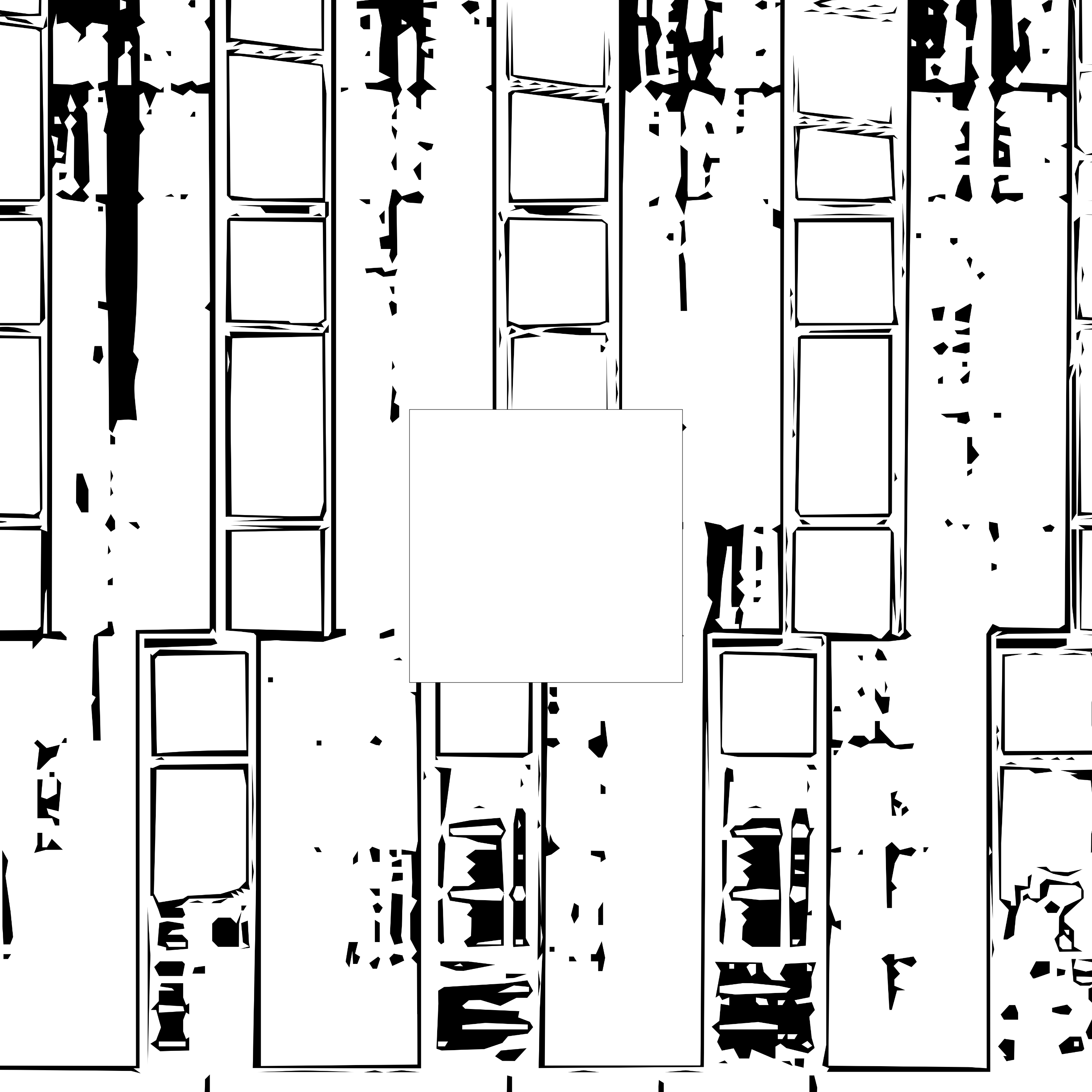
然而4张刚好4倍比例的照片也非常难办。所以事情再次陷入停滞,直到前几天,我突然灵机一动,想到可以把照片跟踪成矢量图,这样就可以随意输出不同分辨率的图片了。于是找了一张以前的照片,在Inkscape里面进行一些加工,得到了这样四幅图:
 |
 |
 |
 |
左上->右上->右下->左下,分别是:大楼,大楼的局部,窗户里,墙上的画。而墙上的画的一部分,正是左上角的大楼。
经过变换之后,分别得到:
 |
 |
 |
 |
由于这些图像本来应该相差四倍,在变换图像上刚好相差90度,所以依次旋转0度,90度,180度,270度之后刚好可以拼贴到一起,结果是这样的:
再把中间的部分去掉,加上自己的签名,是不是有点像那么回事了?
既然做到这个样子了,就忍不住想把讲座中的视频也做出来。结果如下:
持续缩小:
显然,这个山寨的图片距离Escher的原作还有相当差距。对比发现主要问题在于,我基本上是在画中央直接放进去一个自身的1/256,在两个比例之间缺乏意义上的联系。而画面的全部细节都来自第一幅。其他三幅,对应放大4倍、16倍和64倍的时候,缺乏细节。而Escher的原作在不同的尺度上都有丰富的细节。
当然了,做到这个样子我已经很满意了。考虑到Escher的画创作于1956年,数学家大约在2002年揭开其中的奥妙(Chapman是在2002年听了Hendrik Lenstra的发言,受启发决定自己复刻一份,然后在2013年Oxford的数学研究所迁入新大楼的时候拍了照片,制作了视频,2016年在牛津做的讲座。Hendrik Lenstra在2018年的讲座在这里。),艺术家的灵感还是很神奇的。而我能在2020年山寨这么一份儿,似乎也不算很落后:-)。
最后,有没有人能看出来图片中的大楼是什么大楼呢?