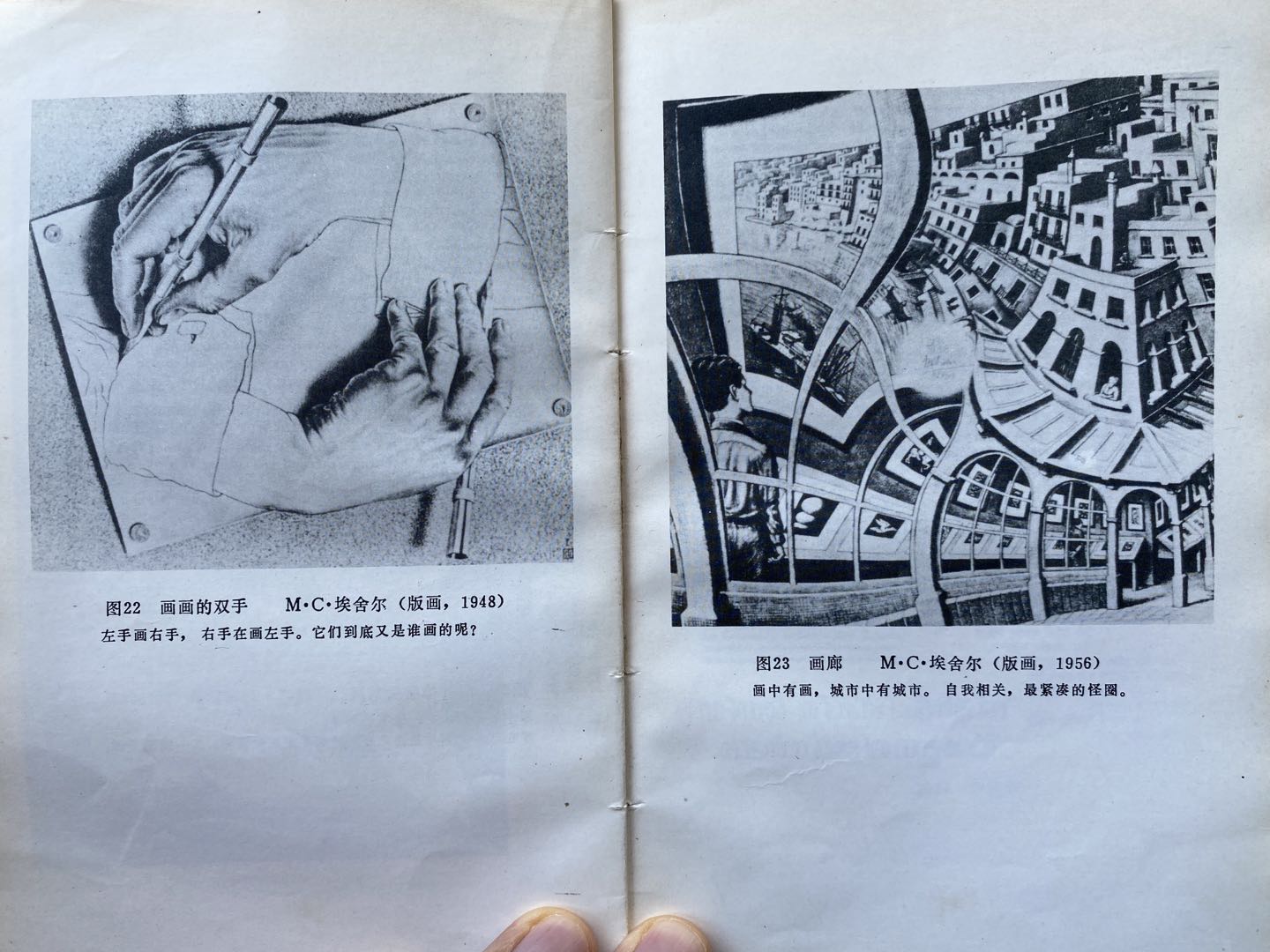
My copy of Escher’s artwork got some attention and quite some people asked me, “what kind of programmer are you?”, well, this Youtube video explains it well.
Actually, Joma’s video basically depicted me when in real dev mode. Upon watching this video, I couldn’t wait to re-implement it in Python. However, the initial version is basically a trans-coding of the original C code and was pretty hard to read. So here is a version that actually uses Matrix multiplication in Python (In the mean time, I still have to fix the syntax highlighter…):
import timeimport numpy as npscreen_size = 40theta_spacing = 0.07phi_spacing = 0.02illumination = np.fromiter(".,-~:;=!*#$@", dtype="<U1")A = 1B = 1R1 = 1R2 = 2K2 = 5K1 = screen_size * K2 * 3 / (8 * (R1 + R2))def render_frame(A: float, B: float) -> np.ndarray:"""Returns a frame of the spinning 3D donut.Based on the pseudocode from: https://www.a1k0n.net/2011/07/20/donut-math.html"""cos_A = np.cos(A)sin_A = np.sin(A)cos_B = np.cos(B)sin_B = np.sin(B)output = np.full((screen_size, screen_size), " ") # (40, 40)zbuffer = np.zeros((screen_size, screen_size)) # (40, 40)cos_phi = np.cos(phi := np.arange(0, 2 * np.pi, phi_spacing)) # (315,)sin_phi = np.sin(phi) # (315,)cos_theta = np.cos(theta := np.arange(0, 2 * np.pi, theta_spacing)) # (90,)sin_theta = np.sin(theta) # (90,)circle_x = R2 + R1 * cos_theta # (90,)circle_y = R1 * sin_theta # (90,)x = (np.outer(cos_B * cos_phi + sin_A * sin_B * sin_phi, circle_x) - circle_y * cos_A * sin_B).T # (90, 315)y = (np.outer(sin_B * cos_phi - sin_A * cos_B * sin_phi, circle_x) + circle_y * cos_A * cos_B).T # (90, 315)z = ((K2 + cos_A * np.outer(sin_phi, circle_x)) + circle_y * sin_A).T # (90, 315)ooz = np.reciprocal(z) # Calculates 1/zxp = (screen_size / 2 + K1 * ooz * x).astype(int) # (90, 315)yp = (screen_size / 2 - K1 * ooz * y).astype(int) # (90, 315)L1 = (((np.outer(cos_phi, cos_theta) * sin_B) - cos_A * np.outer(sin_phi, cos_theta)) - sin_A * sin_theta) # (315, 90)L2 = cos_B * (cos_A * sin_theta - np.outer(sin_phi, cos_theta * sin_A)) # (315, 90)L = np.around(((L1 + L2) * 8)).astype(int).T # (90, 315)mask_L = L >= 0 # (90, 315)chars = illumination[L] # (90, 315)for i in range(90):mask = mask_L[i] & (ooz[i] > zbuffer[xp[i], yp[i]]) # (315,)zbuffer[xp[i], yp[i]] = np.where(mask, ooz[i], zbuffer[xp[i], yp[i]])output[xp[i], yp[i]] = np.where(mask, chars[i], output[xp[i], yp[i]])return outputdef pprint(array: np.ndarray) -> None:"""Pretty print the frame."""print(*[" ".join(row) for row in array], sep="\n")if __name__ == "__main__":for _ in range(screen_size * screen_size):A += theta_spacingB += phi_spacing# clear screen using ANSI control codeprint("\x1b[H")time.sleep(0.05)pprint(render_frame(A, B))