Let’s have a closer look at the encryption. During the communication, what’s been exposed are:
Alice’s public key (n=2627, e=13) , and the encrypted message.
For anyone who’s entered the world of modern cryptography from the old age, it’s tempting to try to decrypt the encrypted message using the encrypting key, the public key.
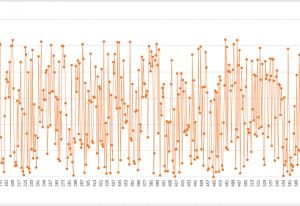
For these people, I have the below chart that shows the mapping between the plain text and the encrypted data:
x-axis is the plain-text data (sorted from 1 to 2627) and y-axis is the encrypted data(from 0 to 2626). I did the calculation using this line of script:
~$ for i in `seq 1 2627`; do echo "$i^13 %2627" | bc; done > /tmp/encryption.mapping
Below is part of this chart zoomed-in:
So you know the encrypted data, let’s say 2144, and you know the public key (n=2627, e=13). How do you find the number x such that x^13 % 2627 = 2144.
You cannot unless you compute everyone possible 1<x<2627 and then find the correct one. That’s brutal force. This is one of the basic assumption behind the security of RSA: There’s no efficient way to find x. This is called the discrete logarithm problem.
In real world scenarios, the 2 prime numbers will be so large that brutal force is simple impractical.
Then to decrypt the message, one would need the private key. The private key is the modular inverse of phi(n). However, in order to get phi(n), he has to know the factors that form n. And factoring large number is mathematically hard. That is the other assumption behind the security of RSA: There’s no efficient way to factor a large number.
As you will see in other places, these 2 assumptions are the corner stones of modern cryptography.
可以。请随意。